Continua dalla pagina precedente
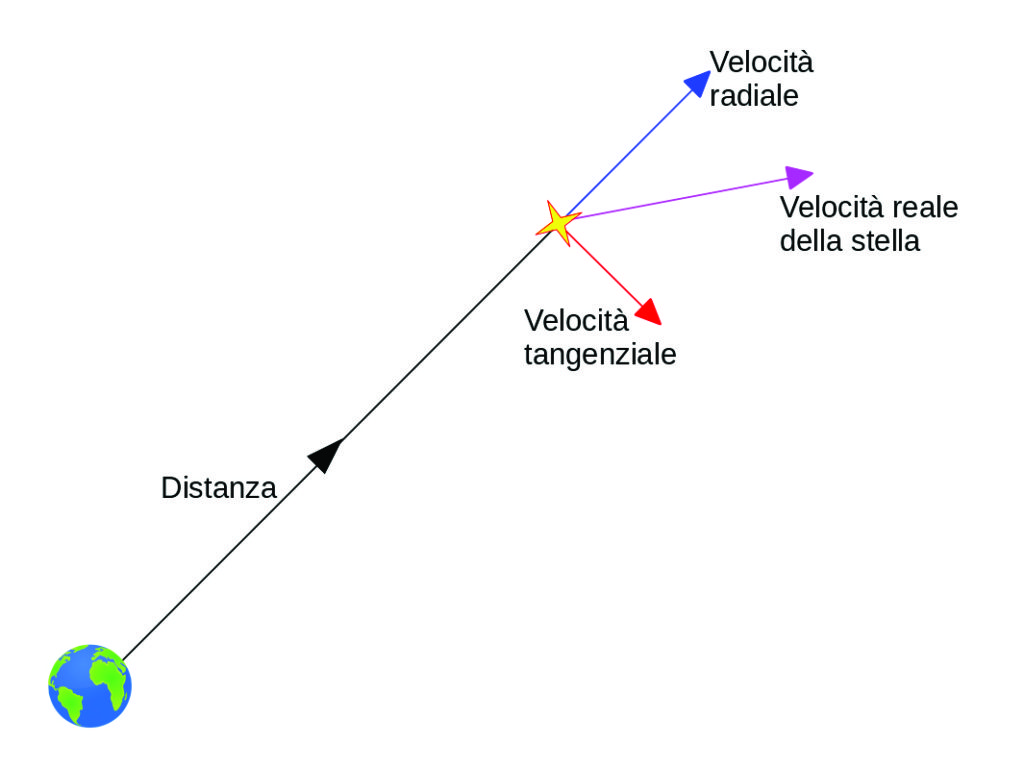
In generale, per stabilire la velocità reale di una stella, è necessario disporre del valore di due componenti, tra loro perpendicolari, quali sono, ad esempio, le velocità tangenziale e radiale (Fig. 11), che avvengono rispettivamente lungo il piano del cielo e lungo la linea di vista, e poi sommarle tra loro “vettorialmente”, ossia tenendo in considerazione, oltre che i valori, anche i loro versi.
La velocità radiale non era misurabile all’epoca di Bessel, mentre per ottenere la velocità tangenziale, dal valore del moto proprio, sarebbe stato necessario conoscere la distanza della stella, perché, a parità di moto proprio, lo spostamento reale e, di conseguenza, la velocità sono tanto maggiori quanto più la stella è lontana. Tuttavia, anche in assenza del valore della distanza, che era proprio quello che Bessel voleva determinare, si può ribaltare il ragionamento di cui sopra, in quanto, a parità di velocità delle stelle lungo la volta celeste, uno spostamento angolare maggiore corrisponde a una distanza minore. Questo era il motivo che aveva indotto Bessel, a ragione, a scegliere come candidata per la misura della parallasse “la stella fuggitiva” del Piazzi, nonostante la scoperta di quest’ultimo, fondata su osservazioni che aveva condotto per ben dieci anni, fosse caduta praticamente nel vuoto e i pochissimi che l’avevano commentata (negativamente) avevano sostenuto che il periodo durante il quale si erano svolte le osservazioni era troppo breve per permettere di trarre delle conclusioni definitive.
Già nel 1812, Bessel aveva pubblicato un articolo, in cui aveva stimato, su basi speculative, un valore pari a 0,46”, per la parallasse annuale della “stella fuggitiva”, assumendo che fosse gravitazionalmente legata alla sua compagna, 61 Cygni B, e ipotizzando dei valori, che aveva ritenuto plausibili, per le masse e i periodi orbitali1Due stelle gravitazionalmente legate orbitano attorno a un punto “fittizio”, detto “centro di massa”. delle due stelle. Da detti valori, aveva derivato, utilizzando la legge di Newton, la distanza tra le due stelle e dal rapporto2Se la distanza tra due stelle lungo il piano del cielo è pari a D e la loro separazione angolare è inferiore a 1°, esprimendo quest’ultima in radianti, Θ, vale la relazione D / d = Θ, dove d è la distanza tra l’osservatore e il sistema delle due stelle. Da tale relazione si ottiene d = D / Θ. tra quest’ultima e la separazione angolare tra le stelle (che aveva misurato al telescopio) aveva ottenuto la distanza del sistema dalla Terra.
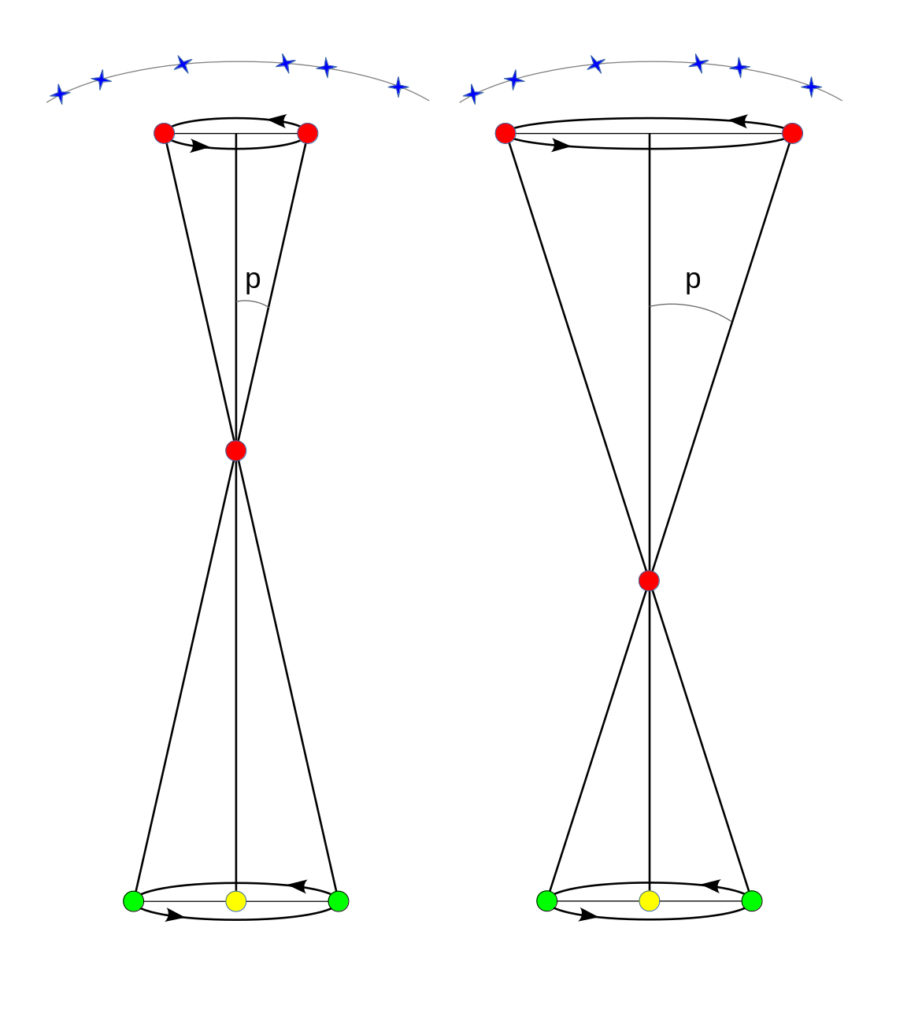
Da essa, aveva stimato il valore della parallasse annuale, p, che, per definizione (Fig. 3),3Fig. 3. Il moto annuale apparente nel cielo di due stelle (D e C) aventi diversa distanza dal Sole (A). La Terra (B) orbita attorno al Sole (A) e tale movimento si riflette nelle stelle in modo tanto più ampio (maggiore per C che per D) quanto più queste sono vicine al sistema Terra-Sole. Le stelle più lontane (E) appaiono, invece, ferme. L’angolo p, indicato nella figura corrisponde a metà dello spostamento angolare totale (mostrato dalle stelle D e C) e, in termini tecnici, è detto “parallasse annuale”. La figura non è in scala: l’angolo p in realtà è estremamente piccolo. è pari alla metà dello spostamento totale mostrato da una stella in riflessione del moto orbitale della Terra ed è legata alla distanza della stella dal sistema Terra-Sole da una relazione molto semplice,
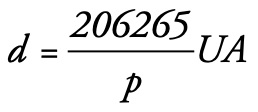
che vede p espressa in secondi d’arco e d in Unità Astronomiche (UA), essendo 1 UA corrispondente alla distanza media tra la Terra e il Sole, pari a circa 150 milioni di chilometri.
Nel 1834, Bessel cominciò a misurare la separazione fra le due stelle del sistema 61 Cygni, con l’eliometro costruito da Fraunhofer. Se il grande moto proprio di 61 Cygni A garantiva la vicinanza con la Terra, erano necessarie, tuttavia, molte osservazioni accurate per trovare in esso la traccia del movimento che avrebbe dovuto riflettere il moto orbitale della Terra e che, in accordo con quanto egli aveva stimato più di 20 anni prima, non avrebbe potuto nemmeno raggiungere il valore di 1”, dal momento che la parallasse annuale è, per definizione, pari a metà dello spostamento corrispondente a due posizioni opposte della Terra nella sua orbita.
Misurare uno spostamento di 1” non era affatto un compito semplice, in quanto tale valore è confrontabile alla dimensione angolare con cui le stelle appaiono scintillare nel cielo per effetto della nostra atmosfera.
Il ritorno della cometa di Halley, fra l’agosto e il novembre dell’anno successivo, catturò l’attenzione di Bessel, costringendolo ad abbandonare la sua campagna di osservazioni su 61 Cygni A, che riuscì a riprendere soltanto due anni dopo, nel 1837. Lungo tutto il corso di quell’anno, egli misurò la separazione tra le due componenti del sistema per decine di volte nell’arco della stessa notte e, alla fine di quella lunga serie di osservazioni, fu in grado di stabilire per la parallasse annuale di 61 Cygni A un valore pari a 0,313”, più piccolo di quello che aveva ipotizzato e un po’ più grande del valore attualmente misurato per la “stella fuggitiva”, che è pari a 0,287”.
Un altro astronomo, tuttavia, era riuscito a misurare la parallasse di una stella poco prima di Bessel. Si trattava di Friedrich Georg Wilhelm von Struve, direttore dell’Osservatorio di Dorpat, che, utilizzando il rifrattore più grande dell’epoca costruito dallo stesso Fraunhofer, aveva trascorso molti anni a misurare, col micrometro filare, le distanze tra le stelle appartenenti a 2.714 sistemi doppi o multipli e aveva pubblicato, nel 1837, i risultati di quel lunghissimo lavoro in un’opera monumentale, intitolata Stellarium Duplicium et Multiplicium Mensurae Micrometricae. Sempre nel corso di quello stesso anno, von Struve aveva annunciato di essere riuscito a misurare la parallasse di Vega, che aveva scelto per la sua luminosità (in quanto tale stella è una delle più brillanti dell’emisfero boreale), per il suo moto proprio abbastanza elevato (pari a 0,35”/anno) e per il fatto che, essendo molto vicina al polo nord dell’eclittica (uno dei due punti di intersezione tra la perpendicolare al piano contenente l’eclittica e la sfera celeste), il suo spostamento durante l’anno sarebbe risultato molto simile a una piccola ellissi.
Il valore rilevato da von Struve risultò 0,125”, straordinariamente simile alla misura attualmente accettata per la parallasse di Vega, pari a 0,127”, tuttavia, quando egli si accorse che Bessel aveva trovato un valore superiore al doppio del suo, che collocava 61 Cygni A a una distanza inferiore alla metà di quella di Vega (come si può evincere dalla relazione tra parallasse e distanza, mostrata nella formula in alto, in questa pagina), temette di aver sbagliato.
Von Struve era consapevole di essersi servito di uno strumento la cui precisione non era paragonabile a quella dell’eliometro e si sentiva, inoltre, molto insicuro del suo risultato, poiché, a differenza di quello di Bessel, era basato soltanto su 17 misure. Così commise l’errore più grande che uno scienziato possa mai fare, ovvero quello di cambiare il valore di una misura, e annunciò per Vega una parallasse revisionata, pari al doppio del valore precedentemente annunciato. Questa terribile ingenuità ebbe come effetto il discredito totale del suo lavoro e fece guadagnare a Bessel il merito di essere stato il primo a misurare la parallasse di una stella.
Fu proprio John Herschel, che all’epoca era presidente della Royal Society, ad assegnare a Bessel la medaglia d’oro per la misura della prima parallasse e nel discorso con cui accompagnò l’assegnazione volle riferirsi anche ad altre due misure avvenute pressoché contemporaneamente a quella di Bessel.
Oltre a quella già citata di von Struve, che a tutti gli effetti aveva preceduto la misura di Bessel ed era stata anche più accurata, ne esisteva una terza a opera di Thomas Henderson. Questi sarebbe potuto risultare il vincitore di quella sfida, che durava da secoli ed era parsa invalicabile, se solo avesse osato un po’ di più. Di origini scozzesi, Henderson aveva lavorato all’Osservatorio Reale del Capo di Buona Speranza e da quel luogo, diversi anni prima dell’annuncio di von Struve e di Bessel, era riuscito a misurare la parallasse di Alpha Centauri, una stella molto luminosa, visibile dall’emisfero australe e caratterizzata da un elevato moto proprio. Alpha Centauri, che a occhio nudo appare come una stella singola, ma in realtà è costituita da due stelle distinte, la A e la B, essendo la seconda un po’ meno luminosa della prima, è per l’esattezza la terza stella in ordine di luminosità dell’emisfero australe: più brillanti di lei risultano soltanto Sirio, visibile anche dall’emisfero boreale, e Canopo, che invece si può vedere nelle regioni settentrionali aventi latitudine inferiore o uguale a 35° 30’, corrispondente, per quanto riguarda l’Italia, all’isola di Lampedusa.
Il valore che Henderson aveva derivato per la parallasse, pari a 1,16”, tuttavia, gli era sembrato eccessivo e, inoltre, egli era consapevole che la sua misura era affetta da un errore abbastanza grande, che aveva stimato essere di 0,11”, per cui, dopo aver controllato più volte il suo risultato, si era deciso ad annunciarlo soltanto nel 1839, giungendo così secondo, dopo Bessel. Henderson non aveva avuto tutti i torti a dubitare della sua misura, poiché, in effetti, aveva sovrastimato la parallasse di Alpha Centauri, che in realtà è significativamente più piccola e pari a 0,747”.
Dalla relazione che lega la parallasse di una stella alla sua distanza dal Sole (riportata qui in basso) si può trovare che gli 0,747” di Alpha Centauri la collocano a 276.124 UA, gli 0,287” di 61 Cygni A a 718.693 UA e i 0,127” di Vega a 1.624.134 UA e che pertanto la stella più vicina, Alpha Centauri, si trova a una distanza che è di quasi 300.000 volte superiore alla distanza media fra la Terra e il Sole. Un valore, quest’ultimo, che Copernico non era riuscito nemmeno a immaginare, in quanto il suo aver collocato le stelle troppo lontane, affinché se ne potesse misurare la parallasse, corrispondeva a una distanza di poco superiore a 1.000 UA, come si può verificare dalla relazione,4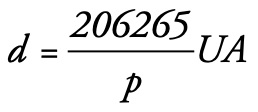 utilizzando per p un valore dell’ordine di 180”, equivalente a 3’, che era quanto di meglio si sarebbe potuto misurare all’epoca, a occhio nudo e senza l’ausilio di un telescopio.
utilizzando per p un valore dell’ordine di 180”, equivalente a 3’, che era quanto di meglio si sarebbe potuto misurare all’epoca, a occhio nudo e senza l’ausilio di un telescopio.
Se volessimo esprimere in chilometri la distanza che ci separa da Alpha Centauri, dovremmo usare un numero costituito da ben 14 cifre, pari all’incirca a 41.420 miliardi di chilometri, che potremmo definire, a ragione, “astronomico” nonostante Alpha Centauri sia una stella molto vicina, così vicina da essere stata considerata, per quasi 100 anni, la stella più prossima al Sole e di conseguenza anche alla Terra.
Nel 1915, un altro astronomo scozzese, Robert Innes, dallo stesso osservatorio in cui aveva operato Henderson, avrebbe scoperto che una stella molto debole e collocata a una notevole distanza angolare (dell’ordine di 2°) da Alpha Centauri A e B aveva un moto proprio del tutto simile a quello delle altre due e, sebbene la separazione angolare rendesse difficile immaginare che la stellina potesse essere gravitazionalmente legata alle due stelle Alpha Centauri, l’uguaglianza dei moti propri era una forte evidenza a sostegno di tale ipotesi. Innes suggerì, pertanto, il nome di Proxima per la stellina, volendo sottintendere con esso proprio l’appartenenza al sistema delle altre due stelle. Due anni dopo, l’astronomo olandese Joan Voûte, direttore dell’Osservatorio Astronomico di Johannesburg, in Sudafrica, sarebbe riuscito a misurare la parallasse della stellina e il nome Proxima si sarebbe rivelato più che azzeccato, anche se non in precisa coerenza con le intenzioni di Innes, in quanto, con la sua parallasse di 0,768” essa rimane a tutt’oggi la stella più vicina al Sole. All’epoca in cui Voûte avrebbe misurato la parallasse di Proxima Centauri, gli astronomi avevano iniziato a utilizzare, da alcuni anni, un’unita di misura per le distanze delle stelle, non solo più adatta a rappresentarle, ma anche più direttamente legata alla parallasse. Era stato l’astronomo inglese Herbert Hall Turner a coniare il termine parsec, risultante dalla contrazione composta delle due parole “parallasse” e “secondo”, proprio per indicare la distanza di una stella, a cui compete una parallasse pari a 1”. Come si può verificare (dalla relazione5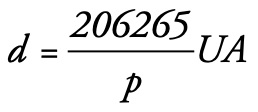 ) a una parallasse p di 1” corrisponde una distanza d di 206.265 UA e quindi 1 parsec (pc) equivale proprio a tale valore e, di conseguenza, il rapporto 1/p fornisce direttamente il valore della distanza d, in parsec.
) a una parallasse p di 1” corrisponde una distanza d di 206.265 UA e quindi 1 parsec (pc) equivale proprio a tale valore e, di conseguenza, il rapporto 1/p fornisce direttamente il valore della distanza d, in parsec.